Rebecca Waldecker - Professorin für Algebra
Forschungsprojekte

Mein Kernarbeitsgebiet ist seit vielen Jahren die Gruppentheorie. Neben lokalen Techniken und Klassifikationsresultaten interessieren mich Anwendungen, bei denen Symmetrie ausgenutzt wird. Alle laufenden Forschungsprojekte sind hier aufgelistet - zuerst die, an denen ich schon lange arbeite, und weiter unten die neueren. Bei den größeren Projekten sind Teilprojekte erwähnt, dazugehörige Abschlussarbeiten und Publikationen.

Strukturtheorie für endliche Gruppen
Dies umfasst Klassifikationsresultate, die von lokalen Bedingungen ausgehen, und auch die Charakterisierung von Gruppen anhand von Eigenschaften des Untergruppenverbandes. Seit meiner Dissertation beschäftige ich mich mit Gruppen, die ein isoliertes Element von Primzahlordnung besitzen. Die Idee dabei ist, ausgehend von solchen isolierten Elementen, ihrem Zentralisator und anderen relevanten lokalen Untergruppen die Struktur der gesamten Gruppe zu verstehen.
Imke Toborg hat über den Spezialfall der Primzahl 3 ihre Doktorarbeit geschrieben, was zu mehreren Publikationen führte.

Einige relevante Veröffentlichungen dazu sind:

Ich habe mehrere Abschlussarbeiten betreut, in denen es darum ging, endliche Gruppen zu klassifizieren, deren Untergruppenverband einen gewissen Verband nicht enthält. Publiziert wurden die Ergebnisse von Juliane Pölzing aus ihrer Masterarbeit, und die Ergebnisse aus der Masterarbeit von Clemens Tietze werden gerade gemeinsam mit Imke Toborg überarbeitet und zur Publikation vorbereitet.
Lucas Pannier hat in seiner Bachelorarbeit (betreut von Imke Toborg) einen Spezialfall von L10-freien Gruppen analysiert.


  • L9-free groups, mit Clemens Tietze und Imke Toborg. In Vorbereitung.
  • Juliane Pölzing und Rebecca Waldecker: M9-free groups, J. Group Theory 18 (2015), 155-190.


Permutationsgruppen, die mit niedriger Fixität wirken
Gemeinsam mit Kay Magaard begann dieses Projekt für mich im Jahr 2012. Die Motivation stammt aus der Theorie der Riemannschen Flächen und ihrer Automorphismengruppen, und es gab bereits Vorarbeiten von Kay Magaard mit Helmut Völklein. Deshalb gab es auch schon mehrere konkrete Vermutungen und Ideen, als ich angefangen habe, mich mit der Fragestellung zu beschäftigen. Was bedeutet es für die Struktur einer Permutationsgrupe, wenn sie transitiv und mit niedriger Fixität wirkt, wenn also jedes nicht-triviale Gruppenelement nur wenige Fixpunkte hat? Dieses Projekt umspannt die Argumentation mit lokalen Methoden ebenso wie eine konkrete Anwendung der Klassifikation der endlichen einfachen Gruppen, bis hin zu der Frage, welche der gefundenen Gruppen(-wirkungen) tatsächlich auf Riemannschen Flächen realisierbar sind. Die Hauptkooperationspartnerin ist momentan Barbara Baumeister.
Patrick Salfeld hat in seiner Dissertation Beiträge sowohl zur Realisierungsfrage als auch zu noch offenen Klassifikationsfragen für Fixität geleistet.
Anika Streck hat im Rahmen dieses Projekts ihre Bachelorarbeit geschrieben (Fixität 2) und arbeitet auch in ihrer Masterarbeit an dem Projekt weiter. Aktuell interessieren wir uns u.a. für den Spezialfall auflösbarer Gruppen, die mit niedriger Fixität wirken, wobei Christoph Möller in seiner Bachelorarbeit die Fälle mit Fixität 2 und 3 bearbeitet hat.
Auch das Promotionsprojekt von Paula Hähndel gehört hier mit dazu, wobei sie für Fixität 4 die ganze Bandbreite abdeckt von Klassifikationsresultaten für einfache Gruppen über allgemeine lokale Argumente bis hin zum Spezialfall auflösbarer Gruppen.
Es gibt eine separate Seite mit GAP-Code, den wir im Rahmen dieses Projekts verwenden. (Noch im Entstehen!)
Einige relevante Publikationen sind:
  • Finite simple permutation groups acting with fixity 4, mit Barbara Baumeister, Paula Hähndel, Kay Magaard, Patrick Salfeld und Anika Streck. In Vorbereitung.
  • The occurrence of finite simple permutation groups of fixity 3 as automorphism groups of Riemann surfaces, mit Patrick Salfeld. Erscheint bei Communications in Algebra.
  • Finite groups of fixity 2 or 3, revisited, mit Paula Hähndel, Christoph Möller und Anika Streck. In Vorbereitung.
  • Patrick Salfeld und Rebecca Waldecker: The occurrence of finite simple permutation groups of fixity 2 as automorphism groups of Riemann surfaces. Journal of Algebra 561 (2020), 402-420. Hier online.
  • Barbara Baumeister, Kay Magaard und Rebecca Waldecker: The Sylow structure of transitive permutation groups acting with fixity 4, Special issue in honor of Kay Magaard, Albanian J. Math. 12 (2018), 137-145. Hier online zu finden.
  • Permutation groups where non-trivial elements have few fixed points. In "Finite Simple Groups: Thirty Years of the Atlas and Beyond", herausgegeben von M. Bhargava, R. M. Guralnick, G. Hiss, K. Lux und P. H. Tiep. Contemporary Mathematics 694, AMS (2017), 223-229.
  • Kay Magaard und Rebecca Waldecker: Transitive permutation groups with trivial four point stabilizers. J. Group Theory 18 (2015), no. 5, 687-740.
  • Kay Magaard und Rebecca Waldecker: Transitive permutation groups where nontrivial elements have at most two fixed points. Journal of Pure and Applied Algebra 219, Issue 4 (2015), 729-759.


Suchalgorithmen für Permutationsgruppen
Dieses Projekt begann 2014 mit Chris Jefferson und Markus Pfeiffer und hat inzwischen zahlreiche Teilprojekte, von denen mehrere in enger Zusammenarbeit mit Chris Jefferson und Wilf Wilson laufen. Manchmal waren oder sind auch Paula Hähndel, Ruth Hoffmann oder Mun See Chang dabei. Die grundsätzliche Idee ist, durch Symmetriebetrachtungen oder die Entwicklung neuer Algorithmen entlang neuer kombinatorischer Strukturen dafür zu sorgen, dass mehr Suchprobleme in Permutationsgruppen mit dem Computer lösbar sind.
Klassische Beispiele sind die Berechnung des Durchschnitts mehrerer Untergruppen von Permutationsgruppen, die Berechnung von Stabilisatoren kombinatorischer Strukturen oder auch die Beantwortung der Frage, ob gewisse Objekte in der gleichen Bahn unter einer Gruppenwirkung liegen. In Computeralgebrasystemen wie GAP oder Magma läuft das darauf hinaus, riesige Mengen von Permutationen systematisch zu durchsuchen. Jede Methode, die den Suchbereich einschränkt oder die Suchschritte beschleunigt, macht Algorithmen schneller bzw. neue Probleme behandelbar, und genau daran arbeiten wir. So haben wir zum Beispiel gezeigt, wie man Orbitalgraphen verwenden kann, um Suchalgorithmen mit Backtrack-Methoden schneller zu machen, oder wie man gleich die ganze Suche entlang von Graphen anstelle von Partitionen organisieren kann. Mit minimalen und kanonischen Bildern kann für zahlreiche Anwendungen erheblicher Rechenaufwand eingespart werden.



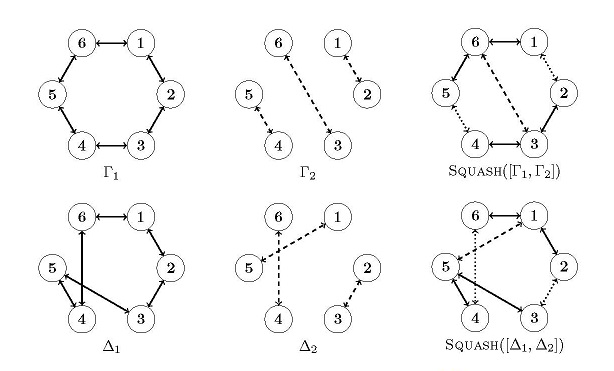
Es gab rund um das Thema Computeralgebra bereits mehrere Abschlussarbeiten, zuletzt von Alexander Klemps, Bastian Schmidt und Paula Hähndel.
Aktuell sind unsere Schwerpunkte die Verbesserung der Implementationen, die Dokumentation dazu, Anwendungen auf die Berechnung von Normalisatoren und Übertragung der Ideen auf die Berechnung kanonischer Bilder.
Publikationen dazu:
  • Perfect refiners for permutation group backtracking algorithms, mit Wurde zur Publikation im Journal of Symbolic Computation akzeptiert, das Manuskript ist im Arxiv verfügbar.
  • Chris Jefferson, Markus Pfeiffer, Rebecca Waldecker und Wilf Wilson: Permutation group algorithms based on directed graphs. Journal of Algebra 585 (2021), 723-758. Hier bereits online zu lesen.
    Link zur "extended version" im Arxiv.
  • Chris Jefferson, Markus Pfeiffer und Rebecca Waldecker: New refiners for permutation groups search. Journal of Symbolic Computation 92 (2019), 70-92. Hier online zu finden.
  • Chris Jefferson, Eliza Jonauskyte, Markus Pfeiffer und Rebecca Waldecker: Minimal and canonical images. Journal of Algebra 521 (2019), 481-506. Hier online zu finden.
  • Paula Hähndel und Rebecca Waldecker: Questions on orbital graphs, In: Davenport J., Kauers M., Labahn G., Urban J. (eds) Mathematical Software - ICMS 2018. Lecture Notes in Computer Science, vol 10931. Springer, Cham. Hier online zu finden.


Die beginnende Tagungstradition am MFO, speziell Gruppentheorie, und die Dynamik hin zum Klassifikationsprojekt
Hier handelt es sich um einen Teilaspekt eines von Volker Remmert, Maria Remenyi und Norbert Schappacher geleiteten DFG-Projekts zur Erforschung der beginnenden Tagungstradition am MFO (Math. Forschungsinstitut Oberwolfach), ungefähr im Zeitraum 1944-1960. Hier gibt es Informationen zum Gesamtprojekt. Ich konzentriere mich auf die Tagungen im Bereich Gruppentheorie oder Gruppen und Geometrien und arbeite heraus, wer die sichtbarsten handelnden Personen waren und welche Themen im Vordergrund standen. Weiter interessiert mich, was für Schätze sich in den Vortragsbüchern und Berichten verstecken und welche Netzwerke sich damals etabliert haben, deren Auswirkungen heute noch erkennbar sind. In diesen Zeitraum fallen aufregende Entwicklungen in der Theorie der endlichen Gruppen, und es entsteht das Momentum, welches zum konkreten Programm für die Klassifikation der endlichen einfachen Gruppen führte. Ein erster schriftlicher Beitrag dazu, was ich im Rahmen dieses Projekts herausgefunden habe, ist in Arbeit, und seit Oktober 2021 läuft das erste Promotionsprojekt im Zusammenhang mit diesem Projekt: ein mathematikhistorischer Blick auf die Entdeckung der modernen sporadischen Gruppen.
Hier gibt es mehr Infos zum Rahmenprojekt.


BEAM: Beyond Amphiphilicity, speziell der algebraische Blick auf die Selbstorganisation von Materialien
Im Rahmen des DFG-Graduiertenkollegs 2670 untersuchen wir die Parkettierungen, die bei der Selbstorganisation gewisser Materialien auftreten. Wie passieren die Übergänge zwischen den verschiedenen Parkettierungstypen, und warum passieren sie so? Welche anderen Parkettierungen können noch realisiert werden, und können wir durch mathematische Beschreibungen besser verstehen, welche Moleküleigenschaften oder Umgebungsparameter wir wie verändern müssen?


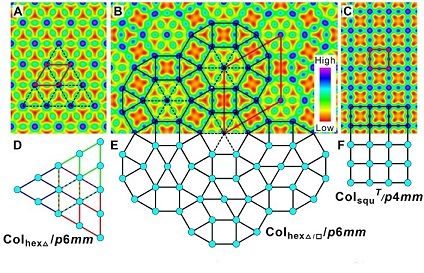
Mehr zum Gesamtprojekt hier, das Teilprojekt gehört zu A3 und ist organisiert in Zusammenarbeit mit Carsten Tschierske.


Zur Startseite.