cantor-logo

"Sie wissen, dass man bis jetzt keinen präzisen Anzahlbegriff für unendliche Mengen hatte. Dies wird wohl auch der Grund sein, warum vor mir Niemand die unendlichen ganzen Zahlen entdeckt hat."

Georg Cantor (1845-1918; seit 1982 Extraordinarius und von 1877 bis 1913 Inhaber eines der damals zwei Lehrstühle für Mathematik an der Friedrichs-Universität in Halle) am 17.12.1982 an den schwedischen Mathematiker Gösta Mittag-Leffler (1846-1927).

Die Grundlagen seiner Theorie unendlicher Mengen entwickelte Georg Cantor während seiner Hallenser Zeit.
Einen wichtigen Schritt auf diesem Weg stellte der Begriff der Gleichmächtigkeit zweier Mengen dar:

Zwei Mengen heißen gleichmächtig, wenn es eine eineindeutige Abbildung der einen
Menge auf die andre Menge gibt.

Der Begriff der Gleichmächtigkeit ermöglicht es insbesondere auch, nichtendliche Mengen miteinander zu vergleichen.
Nach den Peano-Axiomen ist klar, dass die Menge der natürlichen Zahlen mehr als endlich viele Zahlen enthält, also nicht endlich ist. Cantors Überlegungen konzentrierten sich im nächsten Schritt auf die positiven rationalen Zahlen. Das nach ihm benannte sogenannte 1. Diagonalverfahren spiegelt (s)einen Beweisvorschlag für den Nachweis der Gleichmächtigkeit der Menge der natürlichen Zahlen und der Menge der rationalen Zahlen wider. 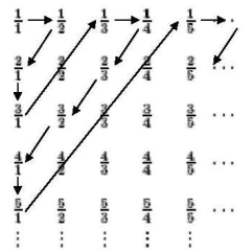Die grundlegende Idee dabei ist es, die positiven rationalen Zahlen in einem zweidimensionalen Schema anzuordnen.

Beweisschritt 1: Man ordnet die positiven rationalen Zahlen in einem zweidimensionalen Schema an:

Beweisschritt 2: Das Logo unseres Instituts zeigt, wie die Zahlen dieses Schemas zu einer Kette „aufgefädelt“ (=angeordnet) werden können.

Um zur Konstruktion für die gesuchte eineindeutige Abbildung dienen zu können, werden nicht vollständig gekürzte Brüche in dieser Kette einfach übersprungen.

Beweisschritt 3: Vermittels dieser Kette kann eine eineindeutige Abbildung zwischen der Menge der natürlichen Zahlen und der Menge der positiven rationalen Zahlen festgelegt werden:

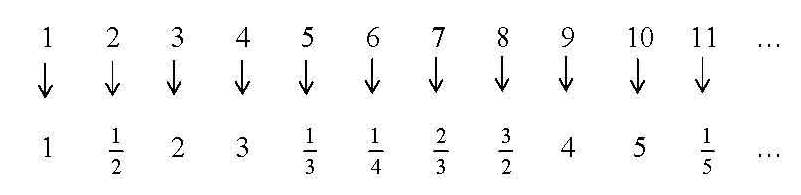
Die nächste Frage, der Cantor sich in diesem Zusammenhang zuwendete, war dem Vergleich der Menge der natürlichen Zahlen und der Menge der reellen Zahlen gewidmet. Er konnte zeigen, dass keine eineindeutige Abbildung der einen auf die andere Menge existiert – mit Hilfe des sogenannten 2. Diagonalverfahrens. In der Sprache der Mächtigkeiten formuliert: Die Mächtigkeit der Menge der natürlichen Zahlen ist echt kleiner als die Mächtigkeit der Menge der reellen Zahlen.

In der Konsequenz hiervon kam es zu seiner berühmten Kontinuumshypothese - der Vermutung Georg Cantors, dass es keine Menge gäbe, die echt größere Mächtigkeit als die Menge der natürlichen Zahlen habe und zugleich aber auch echt kleinere Mächtigkeit als die Menge der reellen Zahlen besitze. Mit der Suche nach einem Beweis seiner Vermutung beschäftigte sich Cantor bis zu seinem Lebensende – in diesem Punkte aber erfolglos. Erst 1963/64 gelang es Paul Cohen (1934-2007), auf bauend auf den Resultaten zur Logik Kurt Gödels (1906-1978), nachzuweisen, dass die Kontinuumshypothese im gebräuchlichen Axiomensystem zur Mengenlehre von Ernst Zermelo (1871-1953) und Abraham Adolf Fraenkel (1891-1965) weder beweis- noch widerlegbar ist.

Literatur-Tipp für eine Monographie, in der die Darstellung der modernen Mengenlehre mit den historischen Überlegungen Cantors verschränkt wird:

Oliver Deiser: Einführung in die Mengenlehre. Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. 3. Auflage. Springer, Berlin / Heidelberg 2010.

Wir danken Torsten Evers für die grafische Umsetzung unserer Idee in der Form, die das Logo jetzt hat. Weiterhin danken wir Prof. Karin Richter für die Recherche und diese Zusamenstellung zum Thema!